Pada artikel mengenai himpunan pembangun, telah diberikan informasi tentang kombinasi linear dari subruang yang dibangun oleh suatu himpunan. Salah satu fakta yang menarik mengenai himpunan pembangun adalah dua himpunan yang berbeda dari suatu ruang vektor dapat membangun ruang vektor yang sama. Contoh sederhana berikut memperlihatkan fenomena tersebut, yaitu
![Rendered by QuickLaTeX.com \[\mathbb{R}^{3}=\left\langle\begin{bmatrix} 1 \\1\\1\end{bmatrix}, \begin{bmatrix} 1\\1\\0\end{bmatrix}, \begin{bmatrix} 1\\0\\0\end{bmatrix}, \begin{bmatrix} 0\\1\\1\end{bmatrix}\right\rangle=\left\langle\begin{bmatrix} 1 \\0\\0\end{bmatrix}, \begin{bmatrix} 0\\1\\0\end{bmatrix}, \begin{bmatrix} 0\\0\\1\end{bmatrix}\right\rangle.\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-5be218e0c287d97fe062953e243e02e0_l3.png)
Pertanyaan:
Jika diberikan sebuah ruang vektor ![]() , apakah terdapat jumlah terkecil dari vektor yang membangun
, apakah terdapat jumlah terkecil dari vektor yang membangun ![]() ?
?
Untuk menjawab pertanyaan di atas, terlebih dahulu diberikan definisi mengenai bebas linear dan bergantung linear.
Definisi:
Misal ![]() adalah ruang vektor atas lapangan
adalah ruang vektor atas lapangan ![]() . Himpunan hingga
. Himpunan hingga ![]() dari vektor dari
dari vektor dari ![]() dikatakan bergantung linear (terhadap
dikatakan bergantung linear (terhadap ![]() ) jika vektor nol adalah kombinasi linear non trivial dari
) jika vektor nol adalah kombinasi linear non trivial dari ![]() , sebaliknya himpunan
, sebaliknya himpunan ![]() disebut bebas linear.
disebut bebas linear.
Berdasarkan definisi di atas, himpunan ![]() adalah sebuah himpunan bergantung linear jika terdapat skalar
adalah sebuah himpunan bergantung linear jika terdapat skalar ![]() yang tidak semua nol sehingga
yang tidak semua nol sehingga
![]()
.
Untuuk kasus sebaliknya, himpunan ![]() adalah sebuah himpunan bergantung linear jika vektor nol hanya dapat dituliskan sebagai kombinasi linear trivial dari vektor-vektor tersebut, yakni jika
adalah sebuah himpunan bergantung linear jika vektor nol hanya dapat dituliskan sebagai kombinasi linear trivial dari vektor-vektor tersebut, yakni jika
![]()
mengakibatkan ![]() .
.
Untuk memperjelas pemahaman mengenai himpunan bebas linear, diperhatikan contoh-contoh berikut ini.
Contoh Himpunan Bergantung Linear:
Himpunan 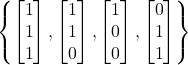 merupakan himpunan bergantung linear (tidak bebas linear) karena terdapat skalar
merupakan himpunan bergantung linear (tidak bebas linear) karena terdapat skalar ![]() dan berlaku
dan berlaku
![Rendered by QuickLaTeX.com \[c_{1}\begin{bmatrix} 1 \\1\\1\end{bmatrix}+c_{2}\begin{bmatrix} 1\\1\\0\end{bmatrix}+c_{3}\begin{bmatrix} 1\\0\\0\end{bmatrix}+c_{4}\begin{bmatrix} 0\\1\\1\end{bmatrix}=\begin{bmatrix} 1 \\1\\1\end{bmatrix}+\begin{bmatrix} 0\\0\\0\end{bmatrix}-\begin{bmatrix} 1\\0\\0\end{bmatrix}-\begin{bmatrix} 0\\1\\1\end{bmatrix}=\begin{bmatrix} 0\\0\\0\end{bmatrix}\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-bcea8b3a5b07b3a0aa6afec011b630ff_l3.png)
Contoh Himpunan Bebas Linear:
Himpunan 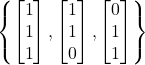 merupakan himpunan bebas linear sebab untuk sebarang skalar
merupakan himpunan bebas linear sebab untuk sebarang skalar ![]() yang memenuhi
yang memenuhi
![Rendered by QuickLaTeX.com \[c_{1}\begin{bmatrix} 1 \\1\\1\end{bmatrix}+c_{2}\begin{bmatrix} 1\\1\\0\end{bmatrix}+c_{3}\begin{bmatrix} 0\\1\\1\end{bmatrix}=\begin{bmatrix} 0\\0\\0\end{bmatrix}\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-13e9fd478095ac1d88722d95ed12d875_l3.png)
berakibat
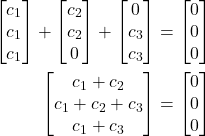
Sehingga diperoleh sistem persamaan linear
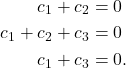
Dari persamaan (1) dan (2), diperoleh nilai ![]() . Selanjutnya dengan mensubstitusikan nilai
. Selanjutnya dengan mensubstitusikan nilai ![]() ke persamaan (3) diperoleh nilai
ke persamaan (3) diperoleh nilai ![]() . Dengan mensubstitusikan nilai
. Dengan mensubstitusikan nilai ![]() ke persamaan (1) diperoleh nilai
ke persamaan (1) diperoleh nilai ![]() . Dengan demikian diperoleh
. Dengan demikian diperoleh ![]() .
.
Izin bertanya, pada contoh mengapa nilai c1=c2=c3=c4 tidak =0? Padahal nilai tersebut memenuhi matriks [0,0,0] dan sangat mudah ditentukan. Terimakasih