Perkalian Matriks
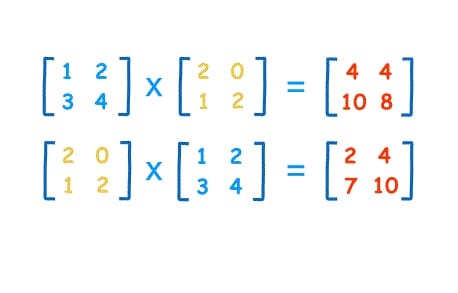
Sebelum membahas mengenai perkalian matriks, berikut ini diberikan definisi untuk beberapa matriks dengan ukuran khusus, yaitu vektor kolom dan vektor baris.
Transpose Matriks
Dalam artikel ini kita akan membahas tentang transpose dari suatu matriks.
Perkalian Skalar dengan Matriks
Selain penjumlahan dua matriks, dikenal juga operasi antara skalar dengan matriks yang definisinya sebagai berikut :
Subruang Vektor
Telah diketahui bahwa himpunan semua bilangan kompleks merupakan ruang vektor atas lapangan bilangan real dan himpunan semua bilangan real merupakan ruang vektor atas dirinya sendiri. Dalam hal ini, ditemukan bahwa ada ruang vektor di dalam ruang vektor yang lain (dengan operasi penjumlahan dan perkalian yang sama). Fenomena ini memunculkan definisi berikut ini.
Penjumlahan Matriks
Dua buah matriks dapat penjumlahan jika ukuran matriks-matriks tersebut sama. Lebih jelasnya diberikan dalam definisi berikut ini.
Apakah Yang Dimaksud Dengan Matriks?
Matriks adalah suatu ekspresi dalam matematika/ susunan bilangan real (atau kompleks) yang disusun dalam baris dan kolom yang dibatasi oleh kurung siku dan dinotasikan sebagai berikut:
Tahukah kamu apa itu ruang vektor?
Sebelum mempelajari ruang vektor, perlu diingat kembali mengenai definisi operasi biner (lihat di sini ) dan definisi grup (lihat di sini). Misalkan adalah suatu lapangan. Suatu ruang vektor atas lapangan