Tahukah kamu apa itu ruang vektor?

Sebelum mempelajari ruang vektor, perlu diingat kembali mengenai definisi operasi biner (lihat di sini ) dan definisi grup (lihat di sini).

Misalkan F adalah suatu lapangan. Suatu ruang vektor atas lapangan F adalah himpunan tak kosong V yang dilengkapi dengan operasi penjumlahan, ditulis dengan ``+'', yang memasangkan setiap pasang  (u,v)\in V\times V secara tunggal dengan obyek  u+v di dalam V dan operasai perkalian skalar, ditulis dengan `` \cdot'', yang memasangkan setiap pasang (r,v)\in F\times V secara tunggal dengan obyek r\cdot v  di dalam V sedemikian hingga 2 operasi tersebut memenuhi aksioma-aksioma berikut:

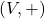  1. (V,+) merupakan grup komutatif,
  2. Untuk setiap 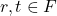r,t\in F, dan setiap 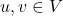u,v\in V, berlaku:
    a.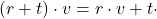 (r+t)\cdot v= r\cdot v+t\cdot
    b.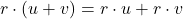 r\c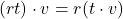d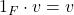ot (u+v)=r\cdot u + r\cdot v
    c. (rt)\cdot v=r(t\cdot v),
    d. 1_{F}\cdot v=v.

Selanjutnya, untuk setiap r\in F dan v\in V, r\cdot v dituliskan dengan rv.

Berikut ini beberapa contoh-contoh ruang vektor.

  1. Himpunan 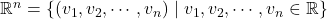\mathbb{R}^{n}=\{(v_{1}, v_{2},\cdots, v_{n})\mid v_{1}, v_{2},\cdots, v_{n}\in \mathbb{R}\} merupakan ruang vektor atas lapangan 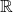\mathbb{R} terhadap operasi penjumlahan dan perkalian skalar 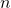n–tuple.
  2. Himpunan semua bilangan kompleks 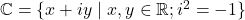\mathbb{C}=\{x+iy \mid x,y\in \mathbb{R}; i^{2}=-1\} merupakan ruang vektor atas lapangan \mathbb{R}.
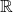  3. Himpunan semua matriks berukuran 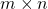m\times n atas bilangan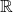 \mathbb{R}

        \[M_{m\times n}(\mathbb{R})=\{A\mid A ~\text{matriks berukuran}~ m\times n ~\text{atas lapangan}~\mathbb{R}\}\]

    merupakan ruang vektor atas lapangan 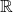\mathbb{R} terhadap operasi penjumlahan matriks dan perkalian skalar dengan matriks.

Tagged , ,