Pada artikel ini, akan dibahas mengenai sistem persamaan linear (SPL) homogen, yakni suatu SPL dimana suku yang memuat konstanta adalah nol. Jadi bentuk umum SPL homogen adalah sebagai berikut :
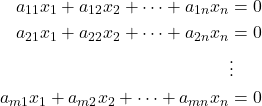
Karena suku konstantanya nol semua, maka sistem persamaan linier homogen ini selalu mempunyai penyelesaian trivial, yaitu
![]()
Pertanyaannya adalah apakah sistem persamaan tersebut juga mempunyai penyelesaian tak nol (non-trivial). Untuk menjawab pertanyaan ini, metode mencari penyelesaian sistem persamaan nonhomogen bisa tetap diterapkan, salah satunya dengan menggunakan metode eleminasi Gauss atau metode eleminasi Gauss-Jordan.
Untuk lebih jelasnya, diperhatikan contoh berikut ini.
Contoh:
Tentukan penyelesaian dari SPL homogen berikut.
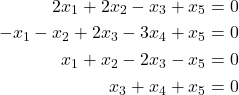
Penyelesaian :
Matrik perluasan dari SPL di atas adalah
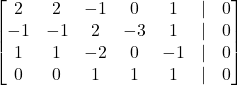
Selanjutnya diselesaikan dengan menggunakan metode operasi Gauss-Jordan.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \begin{bmatrix} 2 & 2 & -1 & 0 & 1 & \mid & 0\\ -1 & -1 & 2 & -3 & 1 & \mid & 0\\ 1 & 1 & -2 & 0 & -1 & \mid & 0\\ 0 & 0 & 1 & 1 & 1 &\mid & 0 \end{bmatrix}\xrightarrow{B_{1} \leftrightarrow B_{3}} &\begin{bmatrix} 1 & 1 & -2 & 0 & -1 & \mid & 0\\ -1 & -1 & 2 & -3 & 1 & \mid & 0\\ 2 & 2 & -1 & 0 & 1 & \mid & 0\\ 0 & 0 & 1 & 1 & 1 &\mid & 0 \end{bmatrix}\\ \xrightarrow[B_{3}+(-2)B_{1}]{B_{2}+B_{1}} &\begin{bmatrix} 1 & 1 & -2 & 0 & -1 & \mid & 0\\ 0 & 0 & 0 & -3 & 0 & \mid & 0\\ 0 & 0 & 3 & 0 & 3 & \mid & 0\\ 0 & 0 & 1 & 1 & 1 &\mid & 0 \end{bmatrix}\\ \xrightarrow[B_{3}\times \frac{1}{3}]{ B_{2}\times \frac{-1}{3}} &\begin{bmatrix} 1 & 1 & -2 & 0 & -1 & \mid & 0\\ 0 & 0 & 0 & 1 & 0 & \mid & 0\\ 0 & 0 & 1 & 0 & 1 & \mid & 0\\ 0 & 0 & 1 & 1 & 1 &\mid & 0 \end{bmatrix}\\ \xrightarrow{ B_{2}\leftrightarrow B_{3}} &\begin{bmatrix} 1 & 1 & -2 & 0 & -1 & \mid & 0\\ 0 & 0 & 1 & 0 & 1 & \mid & 0\\ 0 & 0 & 0 & 1 & 0 & \mid & 0\\ 0 & 0 & 1 & 1 & 1 &\mid & 0 \end{bmatrix}\\ \xrightarrow[B_{4}+(-1)B_{2}+(-1)B_{3}]{ B_{1}+2B_{2}} &\begin{bmatrix} 1 & 1 & 0 & 0 & 1 & \mid & 0\\ 0 & 0 & 1 & 0 & 1 & \mid & 0\\ 0 & 0 & 0 & 1 & 0 & \mid & 0\\ 0 & 0 & 0 & 0 & 0 &\mid & 0 \end{bmatrix}\\ \end{split} \end{equation*}](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-77fcf497c707fe8b688869c861441a9d_l3.png)
Sehingga diperoleh SPL
(1) 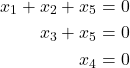
yang berakibat ![]() . Jadi penyelesaian SPL homogen di atas adalah
. Jadi penyelesaian SPL homogen di atas adalah
![]()
dengan ![]() .
.
Lebih lanjut, untuk ![]() diperoleh penyelesaian
diperoleh penyelesaian ![]() . Dengan demikian SPL homogen di atas mempunyai penyelesaian non-trivial.
. Dengan demikian SPL homogen di atas mempunyai penyelesaian non-trivial.