Dalam artikel ini akan diberikan contoh penggunaan metode eleminasi Gauss dalam mencari penyelesaian dari suatu sistem persamaan (lihat di sini untuk melihat definisi sistem persamaan linear).
Bentuk umum sistem persamaan linear pada artikel mengenai definisi SPL, mempunyai matriks yang bersesuaian yang disebut matriks yang diperluas atau augmented matrix sebagai berikut sebagai berikut:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} A \mid b\end{bmatrix} =\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} & \mid b_{1}\\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} & \mid b_{2}\\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots\\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} &\mid b_{m} \end{bmatrix}\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-e1873b7c6d828dea522da539d5c36b0b_l3.png)
Dalam mencari penyelesaian suatu sistem persamaan linear dengan metode eleminasi dan substitusi pada artikel terdahulu (lihat di sini untuk melihat kembali mengenai mencari penyelesaian sistem persamaan linear dengan metode eleminasi dan substitusi), langkah-langkah yang dilakukan dapat dibedakan menjadi ![]() macam, yaitu :
macam, yaitu :
- menukar letak dua persamaan;
- mengalikan suatu persamaan dengan skalar tak nol;
- menambah suatu persamaan dengan kelipatan persamaan yang lain.
Langkah-langkah tersebut berpengaruh pada matriks yang diperluas ![]() yang selanjutnya dikenal dengan sebutan operasi baris elementer yang dibagi menjadi 3, yaitu :
yang selanjutnya dikenal dengan sebutan operasi baris elementer yang dibagi menjadi 3, yaitu :
- menukar letak dua baris;
- mengalikan suatu baris dengan skalar tak nol;
- menambah suatu baris dengan kelipatan baris yang lain.
Operasi-operasi baris elementer tersebut mempunyai tujuan membawa matriks yang diperluas menjadi matriks dengan bentuk lebih sederhana, atau lebih tepatnya dibawa ke bentuk eselon baris (lihat artikel berikut untuk melihat defisini matriks bentuk eselon baris).
Proses menghasilkan bentuk eselon baris ini disebut eliminasi Gauss. Jika matriks yang dihasilkan merupakan matriks bentuk eselon baris tereduksi, prosesnya disebut eliminasi Gauss-Jordan.
Contoh soal :
Tentukan nilai ![]() yang memenuhi sistem persamaan berikut dengan menggunakan metode eleminasi Gauss.
yang memenuhi sistem persamaan berikut dengan menggunakan metode eleminasi Gauss.
(1) 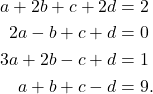
Penyelesaian :
Matriks perluasan dari SPL di atas adalah

Selanjutnya diselesaikan dengan menggunakan metode eleminasi Gauss.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \begin{bmatrix} 1 & 2 & 1 & 2 & | & 2\\ 2 & -1 & 1 & 1 & | & 0\\ 3 & 2 & -1 & 1 & | & 1\\ 1 & 1 & 1 & -1 & | & 9 \end{bmatrix} \xrightarrow[B_{4}+(-1)B_{1}]{B_{2}+(-2)B_{1}, B_{3}+(-3)B_{1}} &\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & -5 & -1 & -3 & \mid & -4\\ 0 & -4 & -4 & -5 & \mid & -5\\ 0 & -1 & 0 & -3 & \mid & 7 \end{bmatrix}\\ \xrightarrow[B_{4}\times (-1)]{B_{2}\times (-1), B_{3}\times (-1)} &\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & 5 & 1 & 3 & \mid & 4\\ 0 & 4 & 4 & 5 & \mid & 5\\ 0 & 1 & 0 & 3 & \mid & -7 \end{bmatrix}\\ \xrightarrow{B_{2} \leftrightarrow B_{4}} &\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & 1 & 0 & 3 & \mid & -7\\ 0 & 4 & 4 & 5 & \mid & 5\\ 0 & 5 & 1 & 3 & \mid & 4 \end{bmatrix}\\ \xrightarrow[B_{4}+(-5)B_{2}]{B_{3}+(-4)B_{2}}&\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & 1 & 0 & 3 & \mid & -7\\ 0 & 0 & 4 & -7 & \mid & 33\\ 0 & 0 & 1 & -12 & \mid & 39 \end{bmatrix}\\ \xrightarrow{B_{3}\leftrightarrow B_{4}} &\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & 1 & 0 & 3 & \mid & -7\\ 0 & 0 & 1 & -12 & \mid & 39\\ 0 & 0 & 4 & -7 & \mid & 33 \end{bmatrix}\\ \xrightarrow{B_{4}+(-4)B_{3}} &\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & 1 & 0 & 3 & \mid & -7\\ 0 & 0 & 1 & -12 & \mid & 39\\ 0 & 0 & 0 & -41 & \mid & 123 \end{bmatrix}\\ \xrightarrow{B_{4}\times \frac {-1}{41}} &\begin{bmatrix} 1 & 2 & 1 & 2 & \mid & 2\\ 0 & 1 & 0 & 3 & \mid & -7\\ 0 & 0 & 1 & -12 & \mid & 39\\ 0 & 0 & 0 & 1 & \mid & -3 \end{bmatrix}\\ \end{split} \end{equation*}](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-aef6bfa31bb09addf83181edb17feb55_l3.png)
Diperoleh sistem persamaan baru
(2) 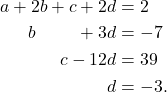
Dengan mensubstitusikan nilai ![]() ke Persamaan ke-2 dan ke-3 pada Sistem Persamaan 2,
ke Persamaan ke-2 dan ke-3 pada Sistem Persamaan 2,
diperoleh nilai ![]() dan
dan ![]() .
.
Selanjutnya, dengan mensubstitusikan nilai ![]() dan
dan ![]() ke Persamaan ke-1 pada Sistem Persamaan 2,
ke Persamaan ke-1 pada Sistem Persamaan 2,
diperoleh nilai ![]() .
.
Jadi penyelesian dari SPL
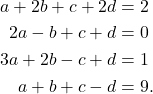
adalah ![]() dan
dan ![]() .
.
*begitu membantu