Tahukah kamu yang disebut basis untuk suatu ruang vektor?
Misalkan V adalah ruang vektor atas lapangan F. Himpunan B disebut basis untuk V jika B membangun V (lihat di sini untuk definisi himpunan pembangun) dan B bebas linear (lihat di sini untuk definisi himpunan bebas linear).
Sebagai contoh himpunan  merupakan basis untuk
merupakan basis untuk ![]() . Lebih lanjut, himpunan
. Lebih lanjut, himpunan ![]() disebut basis standar untuk
disebut basis standar untuk ![]() .
.
Salah satu basis yang lain untuk ![]() adalah
adalah  . Hal ini dikarenakan
. Hal ini dikarenakan ![]() membangun
membangun ![]() dan
dan ![]() merupakan himpunan bebas linear. Berikut ini merupakan ilustrasi pembuktian bahwa himpunan
merupakan himpunan bebas linear. Berikut ini merupakan ilustrasi pembuktian bahwa himpunan ![]() merupakan basis untuk
merupakan basis untuk ![]() .
.
- Himpunan
 membangun
membangun  .
.
Untuk sebarang , berlaku
, berlaku
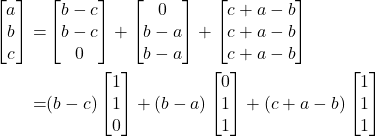
Terbukti bahwa himpunan
 membangun
membangun 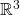 .
. - Himpunan
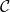 merupakan himpunan bebas linear.
merupakan himpunan bebas linear.
Untuk sebarang bilangan-bilangan real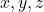 yang memenuhi
yang memenuhi
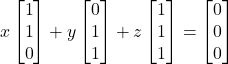
diperoleh
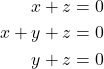
Dengan menyelesaikan SPL Homogen di atas diperoleh
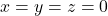 . Jadi terbukti bahwa himpunan
. Jadi terbukti bahwa himpunan  merupakan himpunan bebas linear.
merupakan himpunan bebas linear.
Selanjutnya, berikut ini diberikan syarat perlu dan cukup suatu subhimpunan dari ruang vektor merupakan basis untuk ruang vektor tersebut.
Misalkan ![]() merupakan ruang vektor atas lapangan
merupakan ruang vektor atas lapangan ![]() dan himpunan
dan himpunan ![]() . Himpunan
. Himpunan ![]() merupakan basis untuk
merupakan basis untuk ![]() jika dan hanya jika untuk setiap vektor
jika dan hanya jika untuk setiap vektor ![]() dapat dinyatakan secara tunggal sebagai kombinasi linear dari vektor-vektor
dapat dinyatakan secara tunggal sebagai kombinasi linear dari vektor-vektor ![]() , yakni jika
, yakni jika
![]()
berakibat ![]() untuk setiap
untuk setiap ![]() .
.