Pada artikel ini, akan dibahas mengenai subruang yang dibangun oleh suatu himpunan bagian dari suatu ruang vektor, yakni subruang terkecil yang memuat suatu himpunan bagian tersebut.
Misalkan diberikan ruang vektor ![]() atas lapangan
atas lapangan ![]() dan
dan ![]() himpunan bagian tak kosong dari
himpunan bagian tak kosong dari ![]() . Berdasarkan sifat bahwa irisan dari dua (atau lebih) subruang merupakan subruang, maka dapat dibuktikan bahwa
. Berdasarkan sifat bahwa irisan dari dua (atau lebih) subruang merupakan subruang, maka dapat dibuktikan bahwa
![]()
dengan ![]() subruang di
subruang di ![]() yang memuat
yang memuat ![]() , merupakan subruang terkecil yang memuat
, merupakan subruang terkecil yang memuat ![]() .
.
Pertanyaan: bagaimanakah bentuk elemen-elemen dari ![]() ?
?
Untuk menjawab pertanyaan di atas, terlebih dahulu diperhatikan definisi mengenai kombinasi linear berikut.
Definisi :
Misalkan ![]() adalah ruang vektor atas lapangan
adalah ruang vektor atas lapangan ![]() dan
dan ![]() . Sebarang jumlahan berhingga
. Sebarang jumlahan berhingga
![]()
dengan setiap ![]() , disebut kombinasi linear dari vektor-vektor
, disebut kombinasi linear dari vektor-vektor ![]() . Selanjutnya himpunan
. Selanjutnya himpunan ![]() disebut subruang yang dibangun/direntang oleh
disebut subruang yang dibangun/direntang oleh ![]() dan vektor-vektor
dan vektor-vektor ![]() ;disebut merentang/ membangun U. Sebuah kombinasi linear dikatakan trivial jika semua koefisiennya
;disebut merentang/ membangun U. Sebuah kombinasi linear dikatakan trivial jika semua koefisiennya ![]() dan nontrivial jika minimal terdapat
dan nontrivial jika minimal terdapat ![]() yang bukan nol.
yang bukan nol.
Dengan menggunakan definisi di atas, maka pertanyaan mengenai bentuk elemen-elemen dari ![]() terjawab pada teorema berikut.
terjawab pada teorema berikut.
Teorema :
Misalkan ![]() adalah himpunan bagian tak kosong dari ruang vektor
adalah himpunan bagian tak kosong dari ruang vektor ![]() atas lapangan
atas lapangan ![]() , maka
, maka ![]() , subruang yang dibangun oleh
, subruang yang dibangun oleh ![]() , adalah terdiri dari semua kombinasi linear (berhingga) dari unsur-unsur di
, adalah terdiri dari semua kombinasi linear (berhingga) dari unsur-unsur di ![]() :
:
![Rendered by QuickLaTeX.com \[\langle S\rangle =\left\{\displaystyle \sum_{i=1}^{n} c_{i}x_{i}\mid c_{i}\in F, x_{i}\in S, n\in \mathbb{N}\right\}\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-0192d20a98a5cf4244e7cd5e7b99b332_l3.png)
Bukti:
Misalkan ruas kanan dari persamaan di atas dinotasikan dengan ![]() . Dapat dibuktikan bahwa
. Dapat dibuktikan bahwa ![]() merupakan subruang dari
merupakan subruang dari ![]() . Karena setiap
. Karena setiap ![]() berlaku
berlaku ![]() , maka berdasarlkan definisi
, maka berdasarlkan definisi ![]() , diperoleh
, diperoleh ![]() . Di lain pihak,
. Di lain pihak, ![]() adalah subruang yang memuat
adalah subruang yang memuat ![]() , dengan demikian
, dengan demikian ![]() pasti memuat semua kombinasi linear elemen-elemen dari
pasti memuat semua kombinasi linear elemen-elemen dari ![]() , dengan semikian jelas bahwa
, dengan semikian jelas bahwa ![]() . Jadi terbukti bahwa
. Jadi terbukti bahwa
![Rendered by QuickLaTeX.com \[\langle S\rangle =\left\{\displaystyle \sum_{i=1}^{n} c_{i}x_{i}\mid c_{i}\in F, x_{i}\in S, n\in \mathbb{N}\right\}\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-0192d20a98a5cf4244e7cd5e7b99b332_l3.png)
Contoh Soal:
Diberikan ruang vektor ![]() atas lapangan
atas lapangan ![]() dan himpunan
dan himpunan  . Buktikan bahwa
. Buktikan bahwa
![]()
Penyelesaian:
Jelas bahwa ![]() . Sebaliknya, untuk sebarang
. Sebaliknya, untuk sebarang 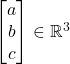 , berlaku
, berlaku
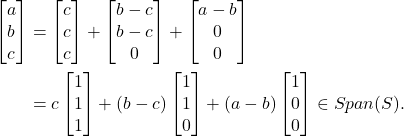
Sehingg diperoleh ![]() . Dengan demikian, terbukti bahwa
. Dengan demikian, terbukti bahwa ![]() .
.
\\\\\\\\