Mencari Penyelesaian Sistem Persamaan Linear Dengan Metode Eleminasi dan Substitusi – Menara Ilmu Aljabar Linear

Dalam artikel ini, akan diberikan contoh penggunaan metode eleminasi dan substitusi dalam mencari penyelesaian dari suatu sistem persamaan (lihat di sini untuk melihat definisi sistem persamaan linear).

Contoh soal :
Tentukan nilai $a,b,c,d$ yang memenuhi sistem persamaan berikut

$\begin{equation*} \begin{split} a + 2b + c + 2d &= 2\\ a - b + c + d &= 0\\ 3a + 2b - c + d &= 1\\ a + b + c - d &= 9. \end{split} \end{equation*}$

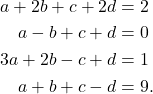
Penyelesaian :

Langkah ke-1 : (persamaan ke-1 digunakan sebagai pivot).

Persamaan ke-2 dikurangkan dengan 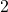$2$ kali persamaan ke-1,
Persamaan ke-3 dikurangkan dengan 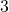$3$ kali persamaan ke-1,
Persamaan ke-4 dikurangkan dengan persamaan ke-1,

diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~~~-5b-c-3d=-4$

$~~~~~~~~~-4b-4c-5d=-5$

$~~~~~~~~~-b~~~~~~-3d=7.$

Langkah ke-2 :

Persamaan ke-2 dikalikan dengan $(-1)$ ,
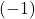Persamaan ke-3 dikalikan dengan $(-1)$ ,
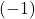Persamaan ke-4 dikalikan dengan $(-1)$ ,

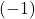diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~~~5b+c+3d=4$

$~~~~~~~~4b+4c+5d=5$

$~~~~~~~b~~~~~~~+3d=-7.$

Langkah ke-3:

Persamaan ke-4 ditukar tempat dengan persamaan ke-2,

diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~b~~~~~~~+3d=-7$

$~~~~~~~~4b+4c+5d=5$

$~~~~~~~~~5b+c+3d=4.$

Langkah ke-4 : (persamaan ke-2 digunakan sebagai pivot).

Persamaan ke-3 dikurangkan dengan 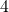$4$ kali persamaan ke-2,
Persamaan ke-4 dikurangkan dengan 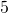$5$ kali persamaan ke-2,

diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~b~~~~~~~+3d=-7$

$~~~~~~~~~4c-7d=33$

$~~~~~~~~~~c-12d=39.$

Langkah ke-5

Persamaan ke-4 ditukar tempat dengan persamaan ke-3,

diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~b~~~~~~~+3d=-7$

$~~~~~~~~~~c-12d=39$

$~~~~~~~~~4c-7d=33.$

Langkah ke-6 : (persamaan ke-3 digunakan sebagai pivot).

Persamaan ke-4 dikurangkan dengan 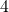$4$ kali persamaan ke-3,

diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~b~~~~~~~+3d=-7$

$~~~~~~~~~~c-12d=39$

$~~~~~~~~~~~~41d=-123.$

Langkah ke-7

Persamaan ke-4 dikalikan dengan $\left(\displaystyle \frac{1}{41}\right)$ ,

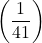diperoleh sistem persamaan baru

$a+2b+c+2d=2$

$~~~~~~~b~~~~~~~+3d=-7$

$~~~~~~~~~~c-12d=39$

$~~~~~~~~~~~~~~d=-3.$

Langkah ke-8

Dengan mensubstitusikan nilai 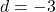$d=-3$ ke persamaan ke-2 dan ke-3,

diperoleh nilai $b=2$ dan $c=3$ .

Langkah ke-9

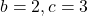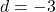Dengan mensubstitusikan nilai $b=2, c=3$ dan $d=-3$ ke persamaan ke-1,

diperoleh nilai $a=1$ .

Jadi, nilai $a,b,c,d$ yang memenuhi sistem persamaan

$a + 2b + c + 2d = 2$

$2a - b + c + d = 0$

$3a + 2b - c + d = 1$

$a + b + c - d = 9$

adalah $a=1, b=2,c=3$ dan $d=-3$ .

Tagged SPL

Leave a Reply Cancel reply