Matriks-matriks Khusus

Pada artikel ini, akan diberikan beberapa jenis matriks-matriks khusus. Matriks-matriks khusus tersebut diantaranya adalah matriks nol, matriks persegi, matriks diagonal, matriks segitiga atas, matriks segitiga bawah,  matriks simetri, matriks bentuk eselon baris, matriks bentuk eselon baris tereduksi. Selanjutnya diperhatikan penjelasan berikut ini:

  1. Matriks Persegi
    Suatu matriks disebut matriks persegi jika matriks tersebut mempunyai jumlah baris dan jumlah kolom yang sama. Berikut ini merupakan contoh-contoh matriks persegi.

        \[\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix}, \begin{bmatrix} 1 & 0 & 3\\ 2 & 1 & -1\\ 1 & 3 & 0 \end{bmatrix}, \begin{bmatrix} 2 & 1 & 0 & 1\\ 3 & 1 & 2 & 2\\ 0 & 2 & 1 & 1\\ -1 & 0 & 1 & 1 \end{bmatrix}, \begin{bmatrix} 2 & 1 & 0 & 1 & 2\\ 3 & 1 & 2 & 2 & 2\\ 0 & 2 & 1 & 1 & 3\\ -1 & 0 & 1 & 1 & 4\\ 2 & 1 & 1 & 2 & 3 \end{bmatrix}.\]

  2. Matriks Diagonal
    Suatu matriks persegi disebut matriks diagonal jika setiap entri-entri yang terletak di luar diagonal utama bernilai nol. Berikut ini merupakan contoh-contoh matriks diagonal.

        \[\begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix}, \begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{bmatrix}, \begin{bmatrix} 2 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 3 \end{bmatrix}, \begin{bmatrix} 3 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 3 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 3 \end{bmatrix}.\]

  3. Matriks Segitiga Atas
    Suatu matriks persegi disebut matriks segitiga atas jika setiap entri-entri yang terletak di bawah diagonal utama bernilai nol. Berikut ini merupakan contoh-contoh matriks segitiga atas.

        \[\begin{bmatrix} 1 & 2 \\ 0 & 2 \end{bmatrix}, \begin{bmatrix} 1 & 3 & 2\\ 0 & 2 & 1\\ 0 & 0 & 3 \end{bmatrix}, \begin{bmatrix} 2 & 2 & 1 & 0\\ 0 & 0 & 1 & 2\\ 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 3 \end{bmatrix}, \begin{bmatrix} 3 & 0 & 1 & 0 & 2\\ 0 & 1 & 3 & 0 & 4\\ 0 & 0 & 3 & 1 & 2\\ 0 & 0 & 0 & 1 & 5\\ 0 & 0 & 0 & 0 & 3 \end{bmatrix}.\]

  4. Matriks Segitiga Bawah
    Suatu matriks persegi disebut matriks segitiga bawah jika setiap entri-entri yang terletak di atas diagonal utama bernilai nol. Berikut ini merupakan contoh-contoh matriks segitiga bawah.

        \[\begin{bmatrix} 1 & 0 \\ 2 & 2 \end{bmatrix}, \begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{bmatrix}, \begin{bmatrix} 2 & 0 & 0 & 0\\ 0 & 2 & 0 & 0\\ 1 & 0 & 1 & 0\\ 1& 2 & 0 & 3 \end{bmatrix}, \begin{bmatrix} 3 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 2 & 1 & 3 & 0 & 0\\ 0 & 0 & 4 & 1 & 0\\ 2 & 0 & 0 & 0 & 3 \end{bmatrix}.\]

  5. Matriks Simetri
    Suatu matriks persegi disebut matriks simetri jika transpose dari matriks tersebut adalah dirinya sendiri. Berikut ini merupakan contoh-contoh matriks simetri.

        \[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \begin{bmatrix} 1 & 2 & 0\\ 2 & 2 & 1\\ 0 & 1 & 3 \end{bmatrix}, \begin{bmatrix} 2 & 2 & 0 & 0\\ 2 & 3 & 1 & 3\\ 0 & 1 & 1 & 5\\ 0& 3 & 5 & 3 \end{bmatrix}, \begin{bmatrix} 3 & 1 & 2 & 0 & 3\\ 1 & 1 & 4 & 1 & 3\\ 2 & 4 & 3 & 5 & 3\\ 0 & 1 & 5 & 1 & 0\\ 3 & 1 & 3 & 0 & 3 \end{bmatrix}.\]

  6. Matriks Bentuk Eselon Baris
    Suatu matriks disebut matriks bentuk eselon baris jika memenuhi kriteria-kriteria berikut:
    1. Entri tak nol pertama pada setiap baris adalah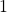 1, yang selanjutnya disebut leading one.
    2. Setiap baris yang memuat leading one, entri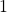 1 terletak disebelah kanan leading one baris sebelumnya.
    3. Baris yang semua entrinya nol (jika ada), terletak di bawah baris yang memuat leading one.Berikut ini diberikan beberapa contoh matriks bentuk eselon baris.

        \[\begin{bmatrix} 1 & 2 & 0\\ 0 & 1 & 1 \end{bmatrix}, \begin{bmatrix} 1 & 2 & 0 & 3\\ 0 & 1 & 1 & 2\\ 0 & 0 & 1 & 2 \end{bmatrix}, \begin{bmatrix} 1 & 2 & 1 & 0\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 1\\ 0& 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 0& 1 & 2 & 0 & 3\\ 0 & 0 & 1 & 1 & 3\\ 0 & 0 & 0 & 1 & 3\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 1 & 1 & 2 & 0 & 3 & 5\\ 0 & 0 & 1 & 2 & 3 & 0\\ 0 & 0 & 0 & 1 & 3 & 2\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}.\]

  7. Matriks Bentuk Eselon Baris Tereduksi
    Suatu matriks disebut matriks bentuk eselon baris jika memenuhi kriteria-kriteria berikut:
    1. Entri tak nol pertama pada setiap baris adalah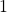 1, yang selanjutnya disebut leading one.
    2. Setiap baris yang memuat leading one, entri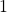 1 terletak disebelah kanan leading one baris sebelumnya.
    3. Baris yang semua entrinya nol (jika ada), terletak di bawah baris yang memuat leading one.
    4. Setiap kolom yang memuat leading one, entri-entri selain leading one adalah nol.Berikut ini diberikan beberapa contoh matriks bentuk eselon baris tereduksi.

        \[\begin{bmatrix} 1 & 0 & 2\\ 0 & 1 & 1 \end{bmatrix}, \begin{bmatrix} 1 & 0 & 0 & 3\\ 0 & 1 & 0 & 2\\ 0 & 0 & 1 & 2 \end{bmatrix}, \begin{bmatrix} 1 & 2 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0& 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 0& 1 & 0& 0 & 3\\ 0 & 0 & 1 & 0 & 3\\ 0 & 0 & 0 & 1 & 3\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 1 & 4 & 0 & 0 & 3 & 5\\ 0 & 0 & 1 & 0 & 3 & 0\\ 0 & 0 & 0 & 1 & 3 & 2\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}.\]