Sebelum membahas mengenai perkalian matriks, berikut ini diberikan definisi untuk beberapa matriks dengan ukuran khusus, yaitu vektor kolom dan vektor baris.
Definisi :
Matriks dengan ukuran ![]() ,
,
![]()
disebut dengan vektor kolom, sedangkan matriks dengan ukuran ![]() ,
,
![]()
disebut vektor baris.
Definisi-definisi tersebut akan digunakan untuk membahas operasi perkalian dua buah matriks dalam artikel ini.
Definisi :
Diberikan matriks ![]() dengan ukuran
dengan ukuran ![]() dan matriks
dan matriks ![]() dengan ukuran
dengan ukuran
![]() . Hasil kali matriks
. Hasil kali matriks ![]() dan
dan ![]() adalah
adalah
![]()
dengan 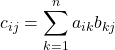 .
.
Perhatikan bahwa ![]() merupakan hasil kali entri-entri baris ke-i matriks
merupakan hasil kali entri-entri baris ke-i matriks ![]() dan kolom ke-
dan kolom ke-
j matriks ![]() . Dua matriks dapat dikalikan jika banyaknya kolom matriks pertama sama
. Dua matriks dapat dikalikan jika banyaknya kolom matriks pertama sama
dengan banyaknya baris matriks kedua.
Untuk lebih memahami mengenai perkalian dua matriks, diperhatikan contoh berikut ini.
Contoh :
Diberikan matriks ![]() dan matriks
dan matriks 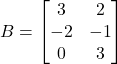 . Akan dihitung hasil kali baris-baris di A dan kolom-kolom di B. Sebagai contoh, akan dihitung hasil kali vektor baris ke-1 dari matriks A dan vektor kolom ke-1 dari matriks B, yang nantinya akan menjadi entri baris ke-1 dan kolom ke-1 dari matriks AB.
. Akan dihitung hasil kali baris-baris di A dan kolom-kolom di B. Sebagai contoh, akan dihitung hasil kali vektor baris ke-1 dari matriks A dan vektor kolom ke-1 dari matriks B, yang nantinya akan menjadi entri baris ke-1 dan kolom ke-1 dari matriks AB.
![Rendered by QuickLaTeX.com \[c_{11}= \begin{bmatrix} 1 & 2 & 3\end{bmatrix}\begin{bmatrix} 3 \\ -2 \\ 0\end{bmatrix}=1\times 3 +2 \times (-2)+3 \times 0 = 3-4+0=-1\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-fed5e0443b61f04bd241eaa411e1d7d9_l3.png)
Langkah-langkah tersebut dilakukan terus terhadap semua vektor-vektor baris matriks A
dan vektor-vektor kolom matriks B, sehingga diperoleh hasil:
![]()
Terkait dengan perkalian matriks, terdapat matriks khusus yang disebut matriks identitas, sebagai berikut:
![Rendered by QuickLaTeX.com \[I_{2}=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}, I_{3}=\begin{bmatrix} 1 & 0 & \\ 0 & 1&0\\ 0 & 0 & 1 \end{bmatrix}, I_{4}=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}.\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-e5d776fc56d3e1527f41439bc323f522_l3.png)
Selanjutnya diberikan sifat-sifat yang diperoleh dari perkalian matriks terhadap operasi-operasi yang lain, yaitu jumlahan dan perkalian dengan skalar.
Sifat-sifat perkalian matriks:
Diberikan matriks ![]() dan
dan ![]() dengan ukuran sedemikian sehingga berlaku
dengan ukuran sedemikian sehingga berlaku
operasi-operasi penjumlahan dan perkalian, ![]() adalah skalar. Pernyataan-pernyataan berikut
adalah skalar. Pernyataan-pernyataan berikut
berlaku:
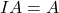 dan
dan 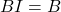 ;
;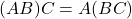 ;
;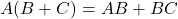 ;
;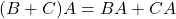 ;
;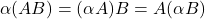 ;
;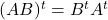 ;
;- Jika
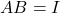 dan
dan 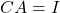 , maka
, maka 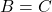 .
.