Dalam artikel ini kita akan membahas tentang transpose dari suatu matriks. Jika matriks
![]()
berukuran ![]() , maka dapat dibentuk matriks baru, sebut saja matriks
, maka dapat dibentuk matriks baru, sebut saja matriks ![]() , yang diperoleh dengan cara merubah baris ke-
, yang diperoleh dengan cara merubah baris ke-![]() matriks
matriks ![]() menjadi kolom ke-
menjadi kolom ke-![]() matriks
matriks ![]() dan merubah kolom ke-
dan merubah kolom ke-![]() matriks
matriks ![]() menjadi baris ke-
menjadi baris ke-![]() matriks
matriks ![]() . Lebih lanjut, matriks
. Lebih lanjut, matriks ![]() dinamakan transpose matriks
dinamakan transpose matriks ![]() , yang dinotasika n dengan
, yang dinotasika n dengan ![]() . Dengan demikian, jika
. Dengan demikian, jika
![]()
maka
![]()
dan ![]() berukuran
berukuran ![]() .
.
Untuk memperjelas pemahaman mengenai transpose matriks, diperhatikan contoh berikut ini.
Contoh:
Diberikan matriks-matriks ![]() dan
dan ![]() sebagai berikut:
sebagai berikut:
![Rendered by QuickLaTeX.com \[A=\begin{bmatrix} 1 & 3 & -2\\ 0 & -2 & 2 \end{bmatrix}, \text{dan}~B=\begin{bmatrix} 2 & -1 & 3 & 2\\ 1 & -1 & -3 & 3\\ 0 & 1 & 2 & -3 \end{bmatrix}.\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-e41be5985ea596709c429fc9e21ef5ef_l3.png)
Transpose matriks ![]() dan
dan ![]() adalah
adalah
![Rendered by QuickLaTeX.com \[A^{t}=\begin{bmatrix} 1 & 0\\ 3 & -2\\ -2 & 2 \end{bmatrix}~\text{dan}~B^{t}=\begin{bmatrix} 2 & 1 & 0\\ -1 & -1 & 1\\ 3 & -3 & 2\\ 2 & 3 & -3 \end{bmatrix}.\]](https://aljabarlinear.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d2d06fa761fd8ac99e0192ff625220b1_l3.png)
Selanjutnya diberikan sifat-sifat yang diperoleh dari suatu transpose matriks terhadap operasi-operasi
yang lain, yaitu jumlahan dan perkalian dengan skalar.
Sifat:
Jika ![]() dan
dan ![]() adalah matriks-matriks dengan ukuran yang sama, dan
adalah matriks-matriks dengan ukuran yang sama, dan ![]() adalah bilangan real (kompleks), maka berlaku
adalah bilangan real (kompleks), maka berlaku
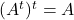
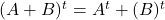
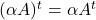 .
.