Dua buah matriks dapat penjumlahan jika ukuran matriks-matriks tersebut sama. Lebih jelasnya diberikan dalam definisi berikut ini.
Definisi:
Diberikan matriks ![]()
dan ![]() yang masing-masing berukuran
yang masing-masing berukuran ![]() . Jumlahan matriks
. Jumlahan matriks ![]() dan
dan ![]() didefinisikan dengan
didefinisikan dengan
![]()
Hasil jumlahan dua matriks berukuran ![]() tersebut berupa matriks berukuran
tersebut berupa matriks berukuran ![]() dengan entri-entrinya merupakan penjumlahan entri-entri matriks
dengan entri-entrinya merupakan penjumlahan entri-entri matriks ![]() dan
dan ![]() yang bersesuaian.
yang bersesuaian.
Untuk lebih jelasnya perhatikan contoh berikut.
Contoh:
Diberikan matriks-matriks ![]() dan
dan ![]() masing-masing berukuran
masing-masing berukuran ![]()
![]()
Jumlahan dari matriks ![]() dan
dan ![]() adalah
adalah
![]()
Selanjutnya, untuk suatu matriks ![]() dapat dibentuk matriks
dapat dibentuk matriks
![]()
Untuk matriks ![]() pada contoh di atas, diperoleh
pada contoh di atas, diperoleh
![]()
Karena penjumlahan matriks melibatkan penjumlahan bilangan-bilangan real pada masing-masing
entrinya, maka sifat-sifat operasi penjumlahan matriks juga dipengaruhi sifat-sifat
operasi penjumlahan bilangan real.
Sifat:
Jika ![]() ,
, ![]() , dan
, dan ![]() adalah matriks-matriks dengan ukuran yang sama, maka berlaku
adalah matriks-matriks dengan ukuran yang sama, maka berlaku
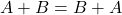
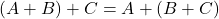
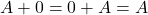
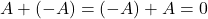 .
.