Apakah Yang Dimaksud Dengan Matriks? – Menara Ilmu Aljabar Linear

Matriks adalah suatu ekspresi dalam matematika/ susunan bilangan real (atau kompleks) yang disusun dalam baris dan kolom yang dibatasi oleh kurung siku dan dinotasikan sebagai berikut:

$A=\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1(n-1)}&a_{1n}\\ a_{21} & a_{22} & a_{23} & \cdots & a_{2(n-1)}&a_{2n}\\ a_{31} & a_{32} & a_{33} & \cdots & a_{3(n-1)}&a_{3n}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{m(n-1)}&a_{mn}\\ \end{bmatrix}.$

Pada definisi di atas, $A$ melambangkan suatu matriks dan matriks tersebut mempunyai baris sebanyak $m$ dan kolom sebanyak $n$ , maka matriks $A$ tersebut dikatakan mempunyai ukuran atau order $m \times n$ dan $a_{ij}$ adalah entri pada baris ke- $i$ dan kolom ke- $j$ untuk setiap $1\leq i \leq m$ dan $1\leq j\leq n$ .

Sebagai contoh, jika matriks 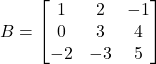$B=\begin{bmatrix} 1 & 2 & -1\\ 0 & 3 & 4\\ -2 & -3 & 5 \end{bmatrix}$ maka matriks $B$ mempunyai ukuran $3\times 3$ dan $b_{11}=1, b_{23}=4$ , dan $b_{32}=-3$ .

Contoh lainnya, jika matriks $C=\begin{bmatrix} -1 & 2 & 3\\ 0 & 1 & -2 \end{bmatrix}$ maka matriks $C$ mempunyai ukuran $2\times 3$ dan $c_{12}=2, c_{21}=0$ , dan $c_{22}=1$ .

Selanjutnya, matriks $A$ bisa dinyatakan secara lebih rinci dengan mendata entri-entrinya
sebagai berikut :

$A =\begin{bmatrix} a_{ij} \end{bmatrix}$

dengan $i=1,2,\cdots, m$ dan $j = 1,2,,\cdots, m$ . Adapun $m$ menyatakan banyaknya baris dan $n$
menyatakan banyaknya kolom matriks $A$ .

Untuk pembahasan selanjutnya, yang dimaksud dengan matriks nol adalah matriks yang semua entrinya adalah $0$ , sebagai contoh

$\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0\\ 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}.$

Tagged materi, matriks